1. 汉诺塔

描述

有三根杆子A，B，C。A杆上有N个(N>1)穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至C杆： 每次只能移动一个圆盘； 大盘不能叠在小盘上面。 提示：可将圆盘临时置于B杆，也可将从A杆移出的圆盘重新移回A杆，但都必须遵循上述两条规则。

问：如何移？最少要移动多少次？

解法

  • 移动函数move()：第n个圆盘，由x盘移到y盘
  • 搜索函数dfs()：将n个圆盘，从x盘->借助y盘->移动到z盘
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
cnt = 0
def move(n: int, x: str, y: str):
    cnt += 1
    print(f"{cnt}: move {n} from {x} to {y}")
    
    
def dfs(n: int, x: str, y: str, z: str):
    if n == 1:
        # 最后一个直接移动到目标
        move(n, x, z)
        return
        
    dfs(n-1, x, z, y)   # 上面的n-1个借助z移到y
    move(n, x, z)   # 底边最后一个直接移动
    dfs(n-1, y, x, z)   # 临时放在y的再借助x移到z


dfs(9, 'A', 'B', 'C')

2. 指数型枚举

描述

从 1∼n 这 n 个整数中随机选取任意多个，输出所有可能的选择方案。

输入一个整数 n。数据范围：1≤n≤15

输出

每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 1 个空格隔开。

对于没有选任何数的方案，输出空行。

解法

选或不选问题，dfs解决。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
n = 10
res = []
vis = [False] * n

def dfs(depth: int):
    if depth == 0:
        # 边界返回
        print(res)
        return
    
    res.append(depth)    # 选第n个数
    dfs(depth - 1)
    res.pop()			# 不选第n个数
    dfs(depth - 1)

dfs(n)

3. 组合型枚举

描述

从 1∼n 这 n 个整数中随机选出 m 个，输出所有可能的选择方案。

输入

两个整数 n,m ,在同一行用空格隔开。

数据范围

n>0 ,

0≤m≤n ,

n+(n−m)≤25

输出

按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行内的数升序排列，相邻两个数用一个空格隔开。

其次，对于两个不同的行，对应下标的数一一比较，字典序较小的排在前面（例如 1 3 5 7 排在 1 3 6 8 前面）。

解法

由于是组合，需要避免重复情况，相对排列需要避免for循环选数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
n = 10
m = 5

res = []
def dfs(depth: int, chosen: int):    # 最大选到n，已经选了chosen个
    if depth == n:
        # 到头了，不能再选，返回
        return
    
    if chosen == m:
        # 选满了，就输出并返回
        print(res)
        return

    res.append(depth+1)   # 选了这个数
    dfs(depth+1, chosen+1)   
    res.pop()  # 不选这个数
    dfs(depth+1, chosen)  # 选下一个数
    
dfs(0, 0)

4. 排列型枚举

描述

把 1∼n 这 n 个整数排成一行后随机打乱顺序，输出所有可能的次序。

输入

一个整数 n。

数据范围

1≤n≤9

输出

按照从小到大的顺序输出所有方案，每行 1 个。

首先，同一行相邻两个数用一个空格隔开。

解法

相对组合，需要考虑逆序，则要进行遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
n = 7

res = []
vis = [False] * n
def dfs(depth: int):
    if depth == n:
        print(res)
        return 
    
    for i in range(n):
        if not vis[i]:      # 如果这个数没被选
            vis[i] = True   # 选上这个数
            res.append(i+1)
            dfs(depth+1)
            res.pop()       # 取消选择，恢复现场
            vis[i] = False
            
dfs(0)  # 从深度0开始搜索

5. 2的幂次方表示

描述

例如 $137=2^7 + 2^3 + 2^0$，写作$2(7)+2(3)+2(0)$。

而括号中的数还可以再展开，如$7=2(2) + 2 + 2(0)$。

输出全部展开的情况。

解法

设想一个函数$dfs()$作用于数字就会让这个数字展开，以$137$为例就是：
$$
dfs(137) = 2dfs(7) + 2dfs(3) + 2dfs(0)
$$
实际上这个等式还可以写作：
$$
dfs(137) = 2dfs(7) + dfs(137-2^7)
$$
根据这个思路就可以写出代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
n = 137

def dfs(x: int) -> str:
    if x <= 0:
        return ''
    if x == 1:
        return '2(0)'
    if x == 2:
        return '2'
    # 以137为例
    x_bin = bin(x)[2:]   # 0b10001001 -> 10001001
    i = len(x_bin) - x_bin.find('1') - 1
    # 对两个dfs做特判
    if i == 0:
        return str(2) + '(0)+' + dfs(x - 2 ** i)
    if i == 1:
        return str(2) + '+' + dfs(x - 2 ** i)
    return str(2) + '(' + dfs(i) + ')+' + dfs(x - 2 ** i)


print(dfs(n))

6. 递归求波兰表达式

描述

  • 平时我们习惯将表达式写成 (1 + 2) * (3 + 4)，加减乘除等运算符写在中间，因此称呼为中缀表达式。
  • 而波兰表达式的写法为 (* (+ 1 2) (+ 3 4))，将运算符写在前面，因而也称为前缀表达式。
  • 逆波兰表达式的写法为 ((1 2 +) (3 4 +) *)，将运算符写在后面，因而也称为后缀表达式。

波兰表达式和逆波兰表达式有个好处，就算将圆括号去掉也没有歧义。上述的波兰表达式去掉圆括号，变为* + 1 2 + 3 4。逆波兰表达式去掉圆括号，变成1 2 + 3 4 + *也是无歧义并可以计算的。事实上我们通常说的波兰表达式和逆波兰表达式就是去掉圆括号的。而中缀表达式，假如去掉圆括号，将 (1 + 2)(3 + 4) 写成 1 + 23 + 4，就改变原来意思了。

1
(2 + 3) * 4`的波兰表示法为`* + 2 3 4

请写程序求解波兰表达式的值。

注意：本题输入的运算符只包括如下4个运算符：+ - * /

输入样例 1 

1
* + 11.0 12.0 + 24.0 35.0

输出样例 1

1
1357.000000

解法

与不同表达式不同的是，波兰表达式计算优先级完全由顺序决定，即：数字立刻与左侧运算符结合。以token为单位对表达式进行解析，定义i为字符串的指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
expr = input() 
tokens = expr.split(' ')   # 空格分隔
i = 0
def solve(exp: str) -> float:
    global i
    cur = exp[i]   # 当前token是什么
    i += 1         # 指向下一个token
    
    if cur in {'+', '-', '*', '/'}:
        # 如果cur是运算符
        left = solve(exp)    # 左边式子
        right = solve(exp)   # 右边式子，由于经过一个solve()导致i已经加1
        if cur == '+':
            return left + right
        if cur == '-':
            return left - right
        if cur == '*':
            return left * right
        if cur == '/':
            return left / right
        
    else:
        # 如果是数字，直接返回
        return float(cur)
    

print(solve(tokens))

7. N皇后问题

描述

输入皇后的个数n（n<=13）

输出长度为n的正整数。

输出结果里的每一行都代表一种摆法。

行里的第i个数字如果是n，就代表第i行的皇后应该放在第n列。

皇后的行、列编号都是从1开始算

解法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
#include<set>

using namespace std;
int n;
string pattern;
vector<string> line;
vector<vector<string>> res;
vector<int> which_column = vector<int>(99, 0);
vector<bool> vis = vector<bool>(99, false);
vector<bool> left_cross = vector<bool>(99, true);    //"/"
vector<bool> right_cross = vector<bool>(99, true);   // "\"
vector<bool> row_avaliable = vector<bool>(99, true);
vector<bool> column_avaliable = vector<bool>(99, true);
void dfs(int depth){
    if(depth == n){
        for(int i = 0; i < n; i++){
            cout<<which_column[i]+1;
        }
        cout<<endl;
        // make_res(which_column, n);
        return;
    }

    for(int i = 0; i < n; i++){
        if(vis[i] == false){
            vis[i] = true;
            if(left_cross[depth + i] == true && right_cross[n + depth - i] == true && row_avaliable[depth] == true && column_avaliable[i] == true){
                left_cross[depth + i] =false;
                right_cross[n+depth-i] = false;
                row_avaliable[depth] = false;
                column_avaliable[i] = false;
                which_column[depth] = i;
                dfs(depth+1);
                which_column[depth] = 0;
                left_cross[depth + i] =true;
                right_cross[n+depth-i] = true;
                row_avaliable[depth] = true;
                column_avaliable[i] = true;
            }
            vis[i] = false;
        }
    }
}

int main(){
    cin>>n;
    dfs(0);
    return 0;
}

8. 排列的逆序数

描述

对于不同的排名结果可以用逆序来评价它们之间的差异。考虑1,2,…,n的排列i1，i2，…，in，如果其中存在j,k，满足 j < k 且ij> ik， 那么就称(ij,ik)是这个排列的一个逆序。一个排列含有逆序的个数称为这个排列的逆序数。例如排列 263451 含有8个逆序(2,1),(6,3),(6,4),(6,5),(6,1),(3,1),(4,1),(5,1)，因此该排列的逆序数就是8。

解法

与逆序相关的算法就是归并排序，并且归并排序保证不进行重复比较，因此可以确保求出逆序数正确。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
nums = [2,6,3,4,5,1]
cnt = 0

def sort(nums: list, left: int, right: int):
    if left >= right:
        return
    
    mid = (left + right) // 2
    i = left
    j = mid + 1
    tmp = []
    
    while i <= mid and j <= right:
        if nums[i] <= nums[j]:
            tmp.append(nums[i])
            i += 1
        else:
            tmp.append(nums[j])
            j += 1
            global cnt
            cnt += mid - i + 1  # 计算逆序对
    
    while i <= mid:
        tmp.append(nums[i])
        i += 1
    
    while j <= right:
        tmp.append(nums[j])
        j += 1
    
    for k in range(len(tmp)):
        nums[left + k] = tmp[k]
         
def merge(nums: list, left: int, right: int):
    if left >= right:
        return
    mid = (left + right) // 2
    merge(nums, left, mid)    # 递归排序左半部分
    merge(nums, mid+1, right)  # 递归排序右半部分
    sort(nums, left, right)   # 合并两个有序数组
    
merge(nums, 0, len(nums)-1)
print(cnt)

其中，逆序数计算为$ cnt = mid-i-1$，这是因为假设左、右子数组是已排序的，如果出现置换(左元素>右元素)，那么左边从这个元素之后一直到mid位置都会大于这个右元素，即构成逆序对。

9. 爬天梯

描述

经过激烈的战斗，林克过关斩将终于抵达初阶递归之试炼的最后一关。
在他面前有一座天梯，天梯的顶端就是传说中的递归试炼通过证了。

林克每步可以跨一级台阶或者跨二级台阶。他必须尝试所有的走法才能得到递归试炼通过证。

如果天梯的台阶数是N，请问他总共需要尝试多少种走法？

输入

输入天梯的台阶数N。

(0<=N<=46)

输出

输出林克有几种走法。

解法

第n级台阶，可以从第n-1级上来，也可以从第n-2级上来，两种情况相互独立，因此方案数：
$$
dp(n) = dp(n-1) + dp(n-2)
\ dp(0) = 1
\ dp(1) = 1
$$

1
2
3
4
5
6
7
8
n = int(input())

dp = [_ for _ in range(n + 10)]
dp[0] = 1
dp[1] = 1
for i in range(2, n + 1):
    dp[i] = dp[i - 1] + dp[i - 2]
print(dp[n])

10. 放苹果

描述

要寻找克罗克果实，林克需要把苹果放在盘子里，其中只有一种情况可以让克罗克果实出现。所以，林克需要尝试所有的放法。

有M个同样的苹果放在N个同样的盘子里，允许有的盘子空着不放，问共有多少种不同的放法？

注意：5，1，1和1，5，1 是同一种放法。

输入

第一行是测试数据的数目t（0 <= t <= 20）。以下每行均包含二个整数M和N，以空格分开。0<=M，N<=10。

输出

对输入的每组数据M和N，用一行输出相应的K。K为正整数，代表共有几种放法。

解法

考虑有$m$个苹果，放$n$个盘子。定义$dp(m, n)$为方案数。初始状态：
$$
dp(0, n) = 1
$$
由于盘子可以为空，但苹果一定有地方放，将$dp(m,n)$划分为两个独立的情况：

  1. 没有空盘子(相当于苹果数减去盘子数)，此时为$dp(m-n, n)$，即剩余苹果分到n个盘子中
  2. 存在空盘子(相当于苹果只在其中n-1个盘子里分，并且其中包含有空盘子的情况)，此时为$dp(m, n-1)$

得到递推式
$$
dp(m, n) = dp(m, n-1) + dp(m-n, n)(m>n)
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
m = 7
n = 3

dp = [[0] * 114 for _ in range(0, 114)]
for i in range(0, n+1):
    dp[0][i] = 1
for i in range(0, m+1):
    for j in range(1, n+1):
        if i < j:
            dp[i][j] = dp[i][i]
        else:
            dp[i][j] = dp[i][j-1] + dp[i-j][j]
        
print(dp[m][n])

11. 林克的命运之阵

描述

每一个人心中都有一个林克。每一个林克都不一样。在命运矩阵里面，随着选择的不同，没有哪一个林克的命运会一模一样。

有一个方格型的命运矩阵，矩阵边界在无穷远处。我们做如下假设：

  1. 每一个格子象征林克命运中的一次抉择，每次只能从相邻的方格中做选择。
  2. 从某个格子出发，只能从当前方格移动一格，走到某个相邻的方格上；

3.选择一旦做出就不可更改，因此走过的格子无法走第二次。

  1. 从命运矩阵的第1行出发，只能向下、左、右三个方向走；

请问：如果最高允许在方格矩阵上走n步（也就是林克一生最多能做n个选择）。
那么随着n的不同，请问一共会有多少种不同选择的方案导致多少个不同的林克？
注意，2种走法只要有一步不一样，即被认为是不同的方案。

输入

允许在方格上行走的步数n(n <= 20)

输出

经过n个选择之后，诞生的不同的林克的个数。

输入样例 1 

1
2

输出样例 1

1
7

输入样例 2 

1
20

输出样例 2

1
54608393

解法

考虑通过走的步数递推。

  • 走0步(不走)，$dp[0] = 1$

  • 走1步，可以下、左、右。$dp[1] = 3$

  • 走2步，在第一步的基础上：

    • 若第一步向下，则第二步向左、右、下均可
    • 若第一步向左，则第二步不能向右；同理，第一步向右，则第二步不能向左

对于第$n$次移动产生的“顶点”，其数量为$dp[n]$，前一次的顶点数为$dp[n-1]$，由于每次移动，对每个顶点，一定有两个方向是可走的，因此有一个分量是$2 * dp[n-1]$。再比较$dp[0],dp[1],dp[2]$的关系，即可得到递推：
$$
dp[n] = 2*dp[n-1] + dp[n-2]
$$

1
2
3
4
5
6
7
8
9
10
n = int(input())

dp = [0] * 114

dp[1] = 3
dp[2] = 7
for i in range(3, 23):
    dp[i] = 2 * dp[i-1] + dp[i-2]
    
print(dp[n])

12. 净化迷雾森林(BFS)

描述

迷雾森林被加农的玷污了，原本圣洁无比的迷雾森林，如今被彻底玷污，空气中充满着紫色的恶臭。

林克临危不惧，带上呼吸面罩，挥舞大师之剑的光芒，净化迷雾。林克所到之处，加农褪去，圣洁回归。

如下图，红色代表墙壁，紫色的迷雾代表需要净化的空间，金色代表林克开始净化的起点。

从某处开始，林克只能向相邻的紫色区域移动。请问，林克总共能够净化多少区域？

输入

包括多个数据集合。每个数据集合的第一行是两个整数W和H，分别表示x方向和y方向瓷砖的数量。W和H都不超过20。

在接下来的H行中，每行包括W个字符。

每个字符表示一个区域的状态，规则如下

1）‘.’：代表紫色迷雾

2）‘#’：代表红墙

3）‘@’：代表林克的起始位(该字符在每个数据集合中唯一出现一次。)

当在一行中读入的是两个零时，表示输入结束。

输出

对每个数据集合，分别输出一行，显示林克从初始位置出发能净化的迷雾数(记数时包括初始位置的迷雾)。

输入样例 1 

1
2
3
4
5
6
7
8
9
10
11
6 9 
....#. 
.....# 
...... 
...... 
...... 
...... 
...... 
#@...# 
.#..#. 
0 0

输出样例 1

1
45

解法

BFS基础题，考虑记录初始点，并向四周扩散。一般思路是：

  1. 将原点入队列，进入循环
  2. 遍历周围点，若可移动就入队列，并标记为已走过
  3. 队列前端元素出队列，继续循环
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<iostream>
#include<string>
#include<vector>
#include<queue>
#include<algorithm>
#include<utility>
#include<cstring>

using namespace std;

int dx[4] = {-1, 1, 0, 0};
int dy[4] = {0, 0, 1, -1};

void print(vector<string> vec){
    for(auto s: vec){
        cout<<s<<endl;
    }
}

int main(){
    int w, h;
    
    while(cin>>w>>h, w || h){
        int cnt = 0;
        int start_x, start_y;
        vector<string> grid(h+2, "0");     // (h+2, w+2)
        vector<vector<bool>> vis(h+2, vector<bool>(w+2, false));
        for(int i = 0; i <= w; i++){
            grid[0] = grid[0] + "0";
            grid[h+1] = grid[h+1] + "0";
        }
        for(int i = 1; i <= h; i++){
            string tmp;
            cin>>tmp;
            tmp = tmp.append("0");
            tmp = tmp;
            if(find(tmp.begin(), tmp.end(), '@') != tmp.end()){
                start_y = find(tmp.begin(), tmp.end(), '@') - tmp.begin() + 1;
                start_x = i;
            }
            grid[i].append(tmp);
        }
        pair<int, int> point(start_x, start_y);
        queue<pair<int, int>> q;
        q.push(point);
        while(!q.empty()){
            cnt++;
            int x = q.front().first;
            int y = q.front().second;
            for(int i = 0; i < 4; i++){
                if(vis[x + dx[i]][y + dy[i]] == false && grid[x + dx[i]][y + dy[i]] == '.'){
                    vis[x + dx[i]][y + dy[i]] = true;
                    q.push(pair<int, int> (x + dx[i], y + dy[i]));
                }
            }
            q.pop();
        }
        cout<<cnt<<endl;
    }
    
    return 0;

}

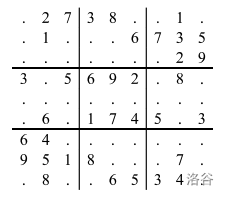
13. 数独(寻找林克的回忆(2))(Lowbit优化)

题目描述

在数独游戏中，给定一个大的 9 × 9 网格，分成了较小的 3 × 3 子网格。例如，

在给定网格中的一些数字后，你的目标是确定剩余的数字，使得数字 1 到 9 恰好出现在以下位置：(1) 九个 3 × 3 子网格中的每一个，(2) 九行中的每一个，以及 (3) 九列中的每一个。

输入格式

输入测试文件将包含多个案例。每个测试案例由一行组成，其中包含 81 个字符，这些字符代表数独网格的 81 个方格，逐行给出。每个字符可以是一个数字（从 1 到 9）或一个句点（用于表示未填充的方格）。你可以假设输入中的每个谜题都有唯一解。文件的结尾由一行包含单词“end”表示。

输出格式

对于每个测试案例，打印一行表示完成的数独谜题。

翻译来自于：ChatGPT

输入输出样例 #1

输入 #1

1
2
3
.2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.
......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
end

输出 #1

1
2
527389416819426735436751829375692184194538267268174593643217958951843672782965341
416837529982465371735129468571298643293746185864351297647913852359682714128574936

解法

位运算

lowbit：返回二进制中1的个数。代码如下：

1
2
3
int lowbit(int x){
    return x & -x;
}

bitmask：二进制掩码，可通过一个9位二进制掩码判断某位数是否可以填在某位。

具体见代码中的注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include<iostream>
#include<string>
#include<vector>
#include<algorithm>
#include<bitset>
#include<cstring>
using namespace std;

const int N = 9;
// 表示每行、每列、各个位数字使用情况，例如：100000000表示这一行/列/格子中只有9是可选的。
int col[N] = {0};
int row[N] = {0};
int box[N/3][N/3] = {0};

int bin_ones[1 << N] = {0};    // 某个十进制数的二进制表示有多少1
int bin_top_one_index[1 << N] = {0};  // 用于记录最高位的1在第几位

string grid;     // 将二维映射至一维

int lowbit(int x){
    return x & -x;    // 获取最低位的1，注意：保持二进制形式，比如1010->0010
}

void init(){
    for(int i = 0; i < N; i++){
        row[i] = col[i] = (1 << N) - 1;
        // 例如N=9, 则： 1000000000 -> 0111111111，9个1
        bin_top_one_index[1 << i] = i;
    }
    for(int i = 0; i < N/3; i++){
        for(int j = 0; j < N/3; j++){
            box[i][j] = (1 << N) - 1;
        }
    }

    for(int i = 0; i < 1 << N; i++){
        bin_ones[i] = 0;
        for(int j = i; j > 0; j -= lowbit(j)){
            bin_ones[i] += 1;
        }
    }
}

int what_number_can_choose(int x, int y){
    // 例如： 1111, 1010, 1110 -> 0010，这个格子只能填2
    return row[x] & col[y] & box[x/3][y/3];   
}

bool dfs(int depth){
    if(depth == 0){
        return true;  // 如果搜索到最底，那一定有解
    }
    int min_choice = 114;    // 最少方案数
    int x, y;

    for(int i = 0; i < N; i++){
        for(int j = 0; j < N; j++){
            // 还有剩余的方案，就开始枚举
            if(grid[i*9+j] == '.'){
                if(min_choice > bin_ones[what_number_can_choose(i, j)]){
                    min_choice = bin_ones[what_number_can_choose(i, j)];
                    x = i;
                    y = j;
                }
            }
        }
    }
    // 找到最优格，开始暴力搜索
    for(int i = what_number_can_choose(x, y); i > 0; i -= lowbit(i)){
        // 在这一位填数字，从低位填起
        row[x] -= 1 << bin_top_one_index[lowbit(i)];
        col[y] -= 1 << bin_top_one_index[lowbit(i)];
        box[x/3][y/3] -= 1 << bin_top_one_index[lowbit(i)];
        grid[x*9 + y] = bin_top_one_index[lowbit(i)] + '1';
        if(dfs(depth-1)){
            return true;
        }
        // 填回来
        row[x] += 1 << bin_top_one_index[lowbit(i)];
        col[y] += 1 << bin_top_one_index[lowbit(i)];
        box[x/3][y/3] += 1 << bin_top_one_index[lowbit(i)];
        grid[x*9 + y] = '.';
    }

    return false;
}

int main(){
    while(cin>>grid, grid[0] != 'e'){
        init();
        int remain = 0;    // 剩余方案数
        // 第一步，记录空位
        for(int i = 0; i < N; i++){
            for(int j = 0; j < N; j++){
                if(grid[i*9 + j] == '.'){
                    // 如果是空格，就加remain，并把这一位设1
                    remain++;
                }else{
                    // 如果是数字，就把对应row、col设为0(已访问)
                    int tmp = grid[i*9 + j] - '1';
                    row[i] -= 1 << tmp;
                    col[j] -= 1 << tmp;
                    box[i/3][j/3] -= 1 << tmp;
                }
            }
        }
        dfs(remain);
        cout<<grid<<endl;
    }
    return 0;
}

14. 靶型数独(寻找林克的回忆(3))

题目描述

小城和小华都是热爱数学的好学生，最近，他们不约而同地迷上了数独游戏，好胜的他们想用数独来一比高低。但普通的数独对他们来说都过于简单了，于是他们向 Z 博士请教，Z 博士拿出了他最近发明的“靶形数独”，作为这两个孩子比试的题目。

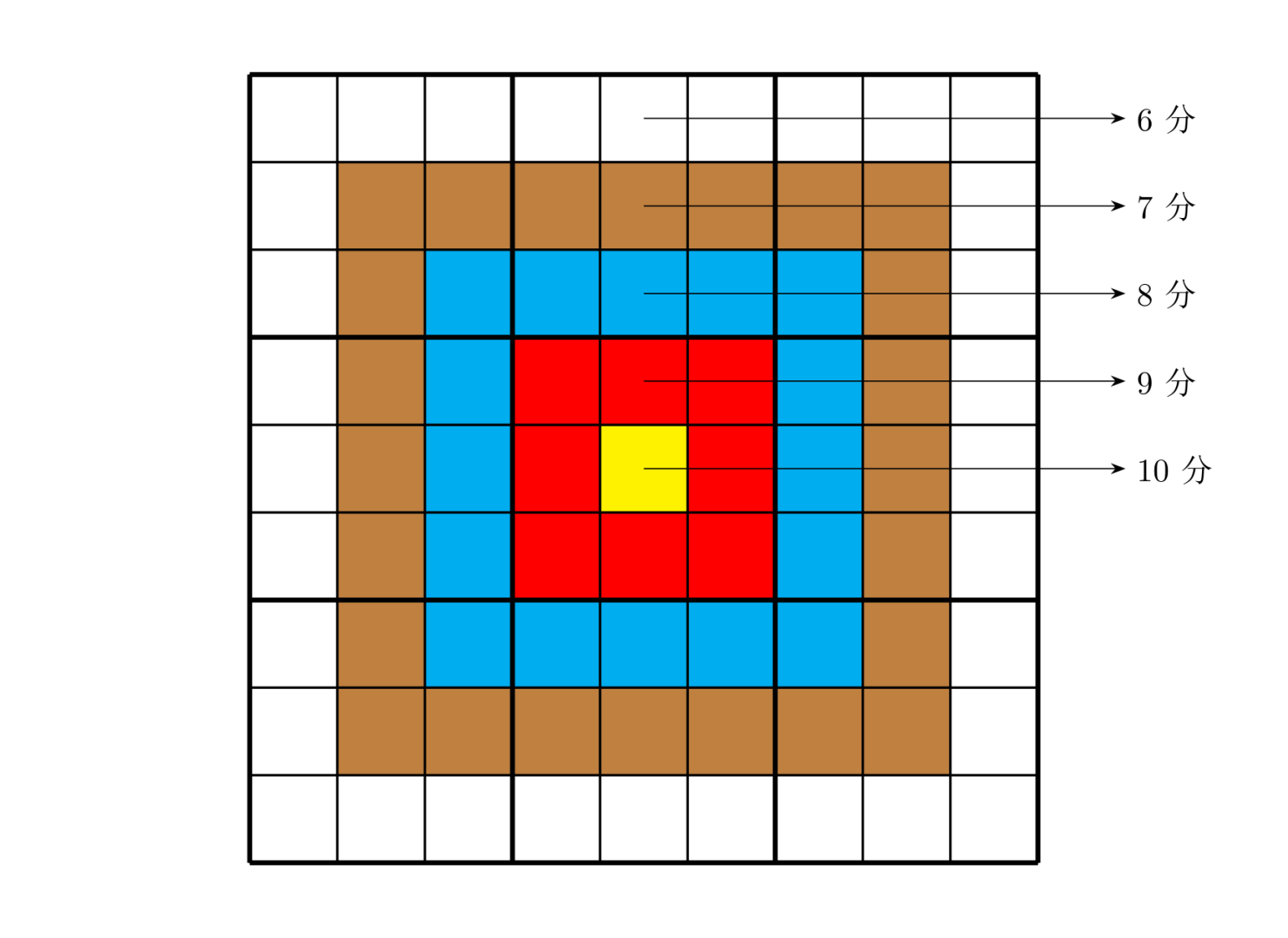
靶形数独的方格同普通数独一样，在 $9$ 格宽且 $9$ 格高的大九宫格中有 $9$ 个 $3$ 格宽且 $3$ 格高的小九宫格（用粗黑色线隔开的）。在这个大九宫格中，有一些数字是已知的，根据这些数字，利用逻辑推理，在其他的空格上填入 $1$ 到 $9$ 的数字。每个数字在每个小九宫格内不能重复出现，每个数字在每行、每列也不能重复出现。但靶形数独有一点和普通数独不同，即每一个方格都有一个分值，而且如同一个靶子一样，离中心越近则分值越高。（如图）

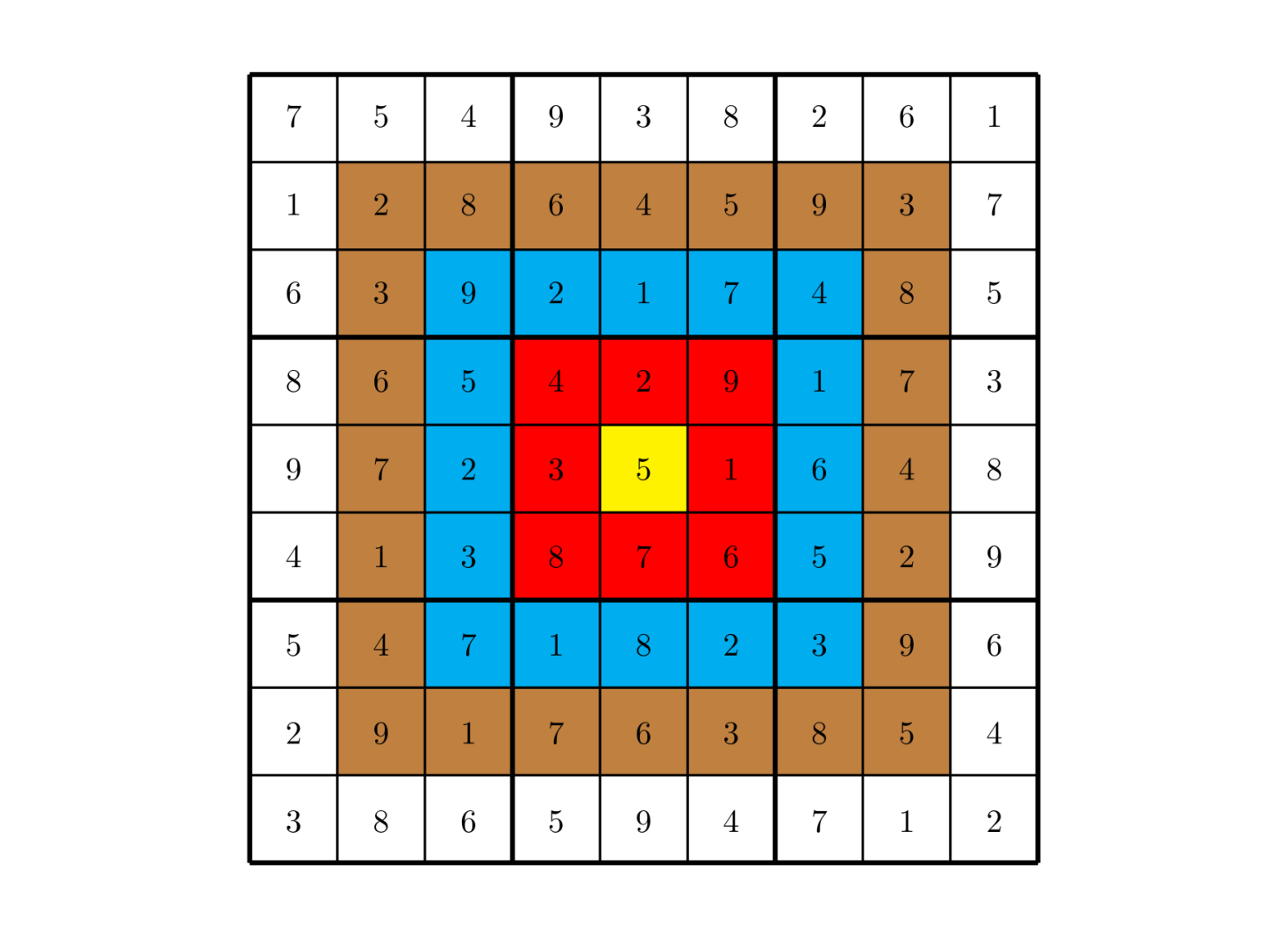
上图具体的分值分布是：最里面一格（黄色区域）为 $10$ 分，黄色区域外面的一圈（红色区域）每个格子为 $9$ 分，再外面一圈（蓝色区域）每个格子为 $8$ 分，蓝色区域外面一圈（棕色区域）每个格子为 $7$ 分，最外面一圈（白色区域）每个格子为 $6$ 分，如上图所示。比赛的要求是：每个人必须完成一个给定的数独（每个给定数独可能有不同的填法），而且要争取更高的总分数。而这个总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和

总分数即每个方格上的分值和完成这个数独时填在相应格上的数字的乘积的总和。如图，在以下的这个已经填完数字的靶形数独游戏中，总分数为 $2829$。游戏规定，将以总分数的高低决出胜负。

由于求胜心切，小城找到了善于编程的你，让你帮他求出，对于给定的靶形数独，能够得到的最高分数。

输入格式

一共 $9$ 行。每行 $9$ 个整数（每个数都在 $0 \sim 9$ 的范围内），表示一个尚未填满的数独方格，未填的空格用“$0$”表示。每两个数字之间用一个空格隔开。

输出格式

输出共 $1$ 行。输出可以得到的靶形数独的最高分数。如果这个数独无解，则输出整数 $-1$。

输入输出样例 #1

输入 #1

1
2
3
4
5
6
7
8
9
7 0 0 9 0 0 0 0 1 
1 0 0 0 0 5 9 0 0 
0 0 0 2 0 0 0 8 0 
0 0 5 0 2 0 0 0 3 
0 0 0 0 0 0 6 4 8 
4 1 3 0 0 0 0 0 0 
0 0 7 0 0 2 0 9 0 
2 0 1 0 6 0 8 0 4 
0 8 0 5 0 4 0 1 2

输出 #1

1
2829

输入输出样例 #2

输入 #2

1
2
3
4
5
6
7
8
9
0 0 0 7 0 2 4 5 3 
9 0 0 0 0 8 0 0 0 
7 4 0 0 0 5 0 1 0 
1 9 5 0 8 0 0 0 0 
0 7 0 0 0 0 0 2 5 
0 3 0 5 7 9 1 0 8 
0 0 0 6 0 1 0 0 0 
0 6 0 9 0 0 0 0 1 
0 0 0 0 0 0 0 0 6

输出 #2

1
2852

说明/提示

数据规模与约定

  • 对于 $40%$ 的数据，数独中非 $0$ 数的个数不少于 $30$；
  • 对于 $80%$ 的数据，数独中非 $0$ 数的个数不少于 $26$；
  • 对于 $100%$ 的数据，数独中非 $0$ 数的个数不少于 $24$。

NOIP 2009 提高组 第三题