题目一：前缀和、动态规划

这是LeetCode第2218题，今天的每日一题。

题面

一张桌子上总共有 n 个硬币 栈 。每个栈有 正整数 个带面值的硬币。

每一次操作中，你可以从任意一个栈的 顶部 取出 1 个硬币，从栈中移除它，并放入你的钱包里。

给你一个列表 piles ，其中 piles[i] 是一个整数数组，分别表示第 i 个栈里 从顶到底 的硬币面值。同时给你一个正整数 k ，请你返回在 恰好 进行 k 次操作的前提下，你钱包里硬币面值之和 最大为多少 。

示例 1：

img

1
2
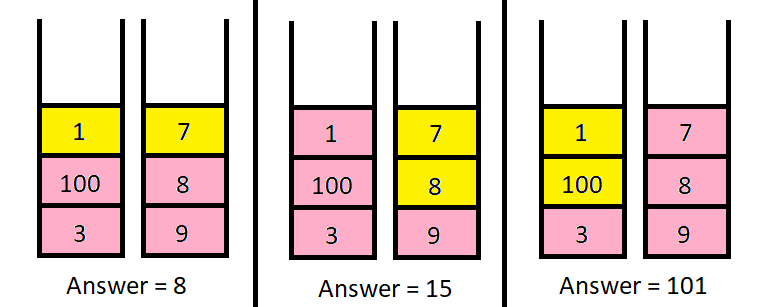
输入：piles = [[1,100,3],[7,8,9]], k = 2
输出：101

思路

首要目标是找到递推关系。

首先确定两个维度。因为取硬币的行为包含两个因素，一个是现在正在取哪一个栈里的硬币，一个是还能取多少硬币。分别记为$i,j$，那么确定：
$$
dp[i][j]
$$
为从前$i$个栈中，至多取出$j$个硬币，面值的最大值。

这个状态由前$i-1$个栈的情况转移而来。如何转移？可以对第$i$个栈中要取多少硬币进行枚举，如果从该栈中取了$w$个，那么之前的$i-1$个栈就至多只能取$j-w$个。取这些情况的最大值，这样一来，状态转移方程就可以确定：
$$
dp[i][j] = max(dp[i-1][j-w]) + v
$$
其中，$v$是第$i$个栈中取$w$个硬币所产生的价值。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int maxValueOfCoins(vector<vector<int>>& piles, int k) {
        vector<vector<int>> dp(2333, vector<int>(2333, 0));
        for(int i = 0; i < piles.size(); i++){
            for(int j = 0; j <= k; j++){
                dp[i+1][j] = dp[i][j];   // 相当于第i+1个栈不取硬币，因为piles[i]的下标最小只有0
                int v = 0;
                for(int w = 1; w <= min((int) piles[i].size(), j); w++){
                    v += piles[i][w-1];   // 获取前缀和
                    dp[i+1][j] = max(dp[i+1][j], dp[i][j-w] + v);
                }
            }
        }
        
        return dp[piles.size()][k];
    }
};

总结

实际上，动态规划就是一种brute force，它隐式地表示了全部最佳情况，并逐一枚举。这是因为仅用贪心算法，其最优解性是难以证明的，而通过对最优解情况的隐式定义，并逐一递推，即可得到结果。